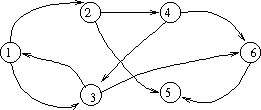
Represented graphically, the graph looks like this:

A graph models many real-life situations, as well as computational concepts. For instance, a graph can model an airport system. Each vertex is an airport, and an edge is a flight from one airport to another. Maybe you can't get from city A to city B since there's no edge, but you can get there by connecting through city C, since edges (A, C) and (C, B) exist.
Note that linked lists are a special kind of graph. So are binary trees, and other multi-way trees. A forest of trees could be considered a single graph. Some graphs, like the one pictured above, represents no possible tree.
The outdegree of a vertex a is the number of edges coming out of a. That is, the outdegree is the number of edges (a, x) in E for any x in V.
The indegree of a vertex a is the number of edges coming into a. That is, the outdegree is the number of edges (x, a) in E for any x in V.
For undirected graphs, there is no indegree and outdegree; there is just the degree: the number of edges incident to a given vertex.
A path between two vertices a and b in a graph is a sequence of vertices a, v1, v2, ..., vn, b such that all of the edges (a, v1), (v2, v3), ..., (vn, b) exist in the graph. In other words, a path is just what it sounds like: a way to get from a to b possibly going through other vertices.
The length of a path is the number of edges encountered on the path. Note that there exists an implicit path of length 0 from any vertex to itself.
A simple path is a path that contains no repeated vertices. In the graph pictures above, 1 -> 3 -> 6 is a simple path. 1 -> 3 -> 1 -> 3 -> 6 is not a simple path. A cycle is a "circular" path (of length greater than 0) that begins and ends on the same vertex. Thus, a simple path is a path containing no cycles. A graph is said to be cylic if it contains cycles, acyclic otherwise.
typedef struct node {
int to, from;
struct node *next;
} edgenode, *graph;
Creating the graph is just setting a pointer equal to NULL.
add_edge is just inserting a node into the linked list:
void add_edge (graph *G, int a, int b) {
edgenode *p;
p = malloc (sizeof (edgenode));
p->to = b;
p->from = a;
p->next = *G;
*G = p;
}
How can we do adjacent_to?
int adjacent_to (graph G, int a, int b) {
edgenode *p;
for (p=G; p; p=p->next)
if (p->from == a && p->to == b) return 1;
return 0;
}
How can we do outdegree?
int outdegree (graph G, int a) {
edgenode *p;
int count;
count = 0;
for (p=G; p; p=p->next)
if (p->from == a) count++;
return count;
}
indegree is not much different.
How about forall_adjacent_to? We could do something like this:
void something (graph G, int a) {
edgenode *p;
for (p=G; p; p=p->next) {
if (p->from == a) {
/* do something */
}
}
}
How about forall_path_to? For instance, maybe we want to
print out every vertex reachable from a given vertex. This is a nontrivial
task. A first try would be something like this:
/* this is wrong! */
void search (graph G, int a) {
for (p=G; p; p=p->next) {
if (p->from == a) {
printf ("%i\n", p->to);
search (G, p->to);
}
}
}
But this will get us into trouble if there are cycles in the graph;
it will just keep going around and around forever. We need to think
of something better. Later on, we'll see Depth First Search and
Breadth First Search: two ways of dealing with this.
By now, we can see that many of the graph operations take time linear in the size of E, i.e., O(|E|). We know from trees and hash tables that we ought to be able to do better.
For a graph G = (V, E), let n = |V|. An adjacency matrix A[n][n] is an array of Boolean values such that A[a][b] is true if and only if the edge (a, b) is in E.
This is a much more time-efficient data structure for holding graphs. For instance, adjacent_to takes only O(1) time, instead of O(|E|). And indegree and outdegree take only O(n) time instead of O(|E|). This is important when there are many more edges than vertices.
However, adjacency matrices require O(n2) storage, where edge lists require only O(|E|) storage.
For some algorithms, such as Warshall's Algorithm (which we will see later), an adjacency matrix works very well.
Note that, with both adjacency matrices and adjacency lists, you have to know beforehand how many vertices there will be. If you don't know, then you can have adjacency lists stored in a linked list instead of an array, so the list can grow. This increases access time to lists, though, since the list has to be chased and that takes longer than accessing an array.
One way of doing this is called depth first search. We start at the first (i.e., lowest numbered) vertex, then "search" that vertex. Searching means to visit that vertex, then recursively search each neighbor (i.e., vertices adjacent from that vertex). The algorithm goes like this:
Depth-First-Search (G) {
unmark each vertex of G
for each vertex a of G {
if (a is unmarked)
Search (G, a)
}
}
Search (G, a) {
mark a as visited.
visit a. // print it or something
for each vertex b adjacent from a {
if (b is unmarked) Search (G, b)
}
}
It's called "depth first" because the Search function goes as
deep as possible, following as many edges as it can, until recursively
returning to visit other vertices.
Each time we go to the next unmarked vertex in Depth-First-Search, we reached all previously unvisited vertices that were unreachable in previous iterations of the loop. So Search gives us a way of doing the forall_path_to operation.
Notice that each time we return to Depth-First-Search from Search, we have traced out a tree embedded in the graph corresponding to the vertices reachable from the previous invokation of Search. The set of trees generated in this way is called the depth first forest of the graph.
For example, the above graph has a depth first forest containing a single tree (since all vertices are reachable from vertex #1). Here is one possible depth first forest for the graph:
1
/ \
3 2
| |
6 4
|
5
If we were to consider vertex #6 as the "first" vertex in the graph,
we would have a different forest (assuming a search order of 6, 1, 2, 3, 4, 5):
6 1
| / \
5 3 2
|
4
Depth first search is a good way of establishing the nature of the
connectivity in a graph. You can build a table out of the results
of a search showing which vertices are reachable from which other vertices.
Depth first search is also used in determining the strongly connected
components of a directed graph. These are all the sub-graphs
in which vertices are mutually reachable.
Another way of going through a graph is breadth first search. As the name implies, it goes wide instead of deep, visiting all vertices adjacent to a given vertex before going on to the next level:
Breadth-First-Search (G) {
initialize a queue Q
unmark all vertices in G
for all vertices a in G {
if (a is unmarked) {
enqueue (Q, a)
while (!empty (Q) {
b = dequeue (Q)
if (b is unmarked) {
mark b
visit b // print or whatever
for all vertices c
adjacent from b {
enqueue (Q, c)
}
}
}
}
}
}
Breadth first search is preferred if we are looking for a vertex
close to another vertex with some property. Also, some graphs are
infinite in size (this might sound hard to believe at first, but it's
true :-). Depth first search gets you nowhere fast in these graphs, but
breadth first search allows you to go one level at a time until you find
what you're looking for.
For example, imagine a chess-playing program. You can think of each possible configuration of the chessboard as a vertex in a graph. The program would do a search in the graph, where moving a particular piece is an edge to another vertex. The program is given, say, 30 seconds to do the search. Using depth first search would allow the program to explore many moves ahead for one particular initial move, but wouldn't allow it to explore any other moves. Breadth first search would allow a variety of moves to be explore, up to several moves ahead.
This program demonstrates an implementation of graphs and these two searching algorithms. The graphs have integer vertices numbered starting from 0, and use adjacency lists:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "queue.h" /* some integer queue functions */
/* linked list node for adjacency lists */
typedef struct list {
int v; /* there is an edge to this vertex */
struct list *next;
} listnode;
typedef struct _graph {
int n; /* number of vertices */
listnode **adjlists; /* will be an array of lists */
int *marks; /* array of Boolean */
} graph;
/* create an empty graph, knowing a priori how many vertices there will be */
void create_graph (graph *G, int n) {
int i;
G->n = n;
G->adjlists = malloc (n * sizeof (listnode *));
G->marks = malloc (n * sizeof (int));
for (i=0; i<n; i++) G->adjlists[i] = NULL;
}
/* insert a new edge to b into the adjacency list for a */
void insert_edge (graph *G, int a, int b) {
listnode *p;
/* standard linked list insertion on adjlists[a] */
p = malloc (sizeof (listnode));
p->v = b;
p->next = G->adjlists[a];
G->adjlists[a] = p;
}
/* "search" the graph from vertex 'a' to all vertices reachable from 'a' */
void search (graph G, int a) {
listnode *p;
int i, b;
G.marks[a] = 1;
printf ("%i\n", a);
for (p=G.adjlists[a]; p; p=p->next) {
b = p->v;
if (!(G.marks[b])) search (G, b);
}
}
/* Depth First Search
* search the graph beginning with the first vertex, until all vertices
* have been visited
*/
void dfs (graph G) {
int a;
/* set all marks to False */
memset (G.marks, 0, G.n * sizeof (int));
/* for all vertices, search from that vertex */
for (a=0; a<G.n; a++)
if (!(G.marks[a])) search (G, a);
}
void bfs (graph G) {
queue Q;
int a, b;
listnode *p;
/* initialize queue */
create_queue (&Q);
/* set all marks to False */
memset (G.marks, 0, G.n * sizeof (int));
/* for each vertex in the graph */
for (a=0; a<G.n; a++) {
if (!(G.marks[a])) {
enqueue (&Q, a);
/* keep dequeueing until empty queue */
while (!emptyq (Q)) {
b = dequeue (&Q);
if (!(G.marks[b])) {
/* visit this unmarked vertex */
G.marks[b] = 1;
printf ("%i\n", b);
/* enqueue all its neighbors */
for (p=G.adjlists[b]; p; p=p->next)
enqueue (&Q, p->v);
}
}
}
}
}
int main () {
graph G;
/* make the graph given in the lecture notes */
create_graph (&G, 7);
insert_edge (&G, 1, 2);
insert_edge (&G, 1, 3);
insert_edge (&G, 2, 4);
insert_edge (&G, 2, 5);
insert_edge (&G, 3, 1);
insert_edge (&G, 3, 6);
insert_edge (&G, 4, 6);
insert_edge (&G, 4, 3);
insert_edge (&G, 6, 5);
dfs (G);
bfs (G);
}