Lecture 11
Dynamic Programming
Dynamic programming is a method frequently applied to
optimization problems, problems where we are looking for the
best solution to a problem.
A famous example of an optimization problem is the "travelling salesman
problem." A travelling salesman must visit n cities and return
to the first city, minimizing the cost of his tour (in terms of gallons
of gasoline used, miles travelled, or some other metric). An optimal
solution is one that is no longer than any other solution (we can't
say "shortest" because there may be more than one solution with the same
length). We will see this problem again later in the semester when
we study NP-complete problems.
Developing a dynamic programming algorithm consists of these steps:
- Characterize the structure of an optimal solution.
- Recursively define the value of an optimal solution.
- Compute the value of an optimal solution in a bottom-up fashion.
- Construct an optimal solution from computed information.
Not all problems easily lend themselves to this approach. For example,
the problem of sorting (which can be thought of as optimizing the degree
of disorder in an array according to some proper definition of disorder)
is best done using a divide-and-conquer approach, even though on the
surface each of the four steps above seems to apply.
Dynamic programming is best applied to problems having these two
characteristics:
- Optimal substructure.
Consider a problem P, broken down into two subproblems,
P1 and P2. We must be able
to efficiently combine optimal solutions to P1
and P2 into an optimal solution to P.
The structure of an optimal solution must contain optimal solutions to
the recursive subproblems.
- Overlapping subproblems.
Having defined in the second step the value of an optimal solution,
a first attempt at solving the problem may be to simply implement
a solution as a recursive algorithm. Dynamic programming requires
that the recursive sub-solutions be computed many times, i.e. that the
straight recursive solution does a lot of unnecessary computation.
Dynamic programming works by eliminating this redundancy.
Your book gives matrix-chain multiplication as the first example of
dynamic programming. Before we dive into this rather involved problem,
let's look at a very simple example, to get the feel for dynamic
programming.
Suppose you want to compute the nth Fibonacci number,
Fn. The optimal solution to the problem
is simply Fn (this is a somewhat contrived
use of the word "optimal" to illustrate dynamic programming :-).
Recall that the Fibonacci numbers are defined:
F(n) =
1, if n=1 or 2,
Fn-2 + Fn-1 otherwise.
So the Fibonacci numbers are:
n : 1 2 3 4 5 6 7 8 9 10 ...
F_n: 1 1 2 3 5 8 13 21 34 55 ...
Thus we have completed steps 1 and 2 for designing a dynamic programming
algorithm to compute Fn. We are prepared
to write a non-dynamic algorithm as simply:
F (n)
if (n = 1) or (n = 2) then return 1
return F(n-2) + F(n-1)
This is not an efficient algorithm for computing Fn.
Let's look at the recursive calls made for F4:
F(5)
/ \
/ \
/ \
/ \
/ \
/ \
/ \
F(3) + F(4)
/ \ / \
/ \ / \
F(2) + F(1) F(2) + F(3)
| | | / \
1 1 1 F(1)+F(2)
| |
1 1
Note that F2 is computed three times,
and F3 is computed twice. Each recomputation incurs
extra recusive work that has already been done elsewhere.
Note also the shape of this diagram; it looks like a binary tree of
calls. We can see the height of the tree by going from the root to the
rightmost leaf. The height is
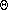 (n).
(n).
The tree is not complete, but it is very full. What do we know about complete
binary trees of height n? They have 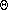 (2n) nodes. While this tree is not quite that big, it is
very close. There are Fn 1's as leaves of the
tree, so at least that many additions. From equation 2.15 in the book,
we can tell that Fn =
(2n) nodes. While this tree is not quite that big, it is
very close. There are Fn 1's as leaves of the
tree, so at least that many additions. From equation 2.15 in the book,
we can tell that Fn =
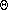 (
( n), where
n), where  is the Golden Ratio, about 1.618033988, so this algorithm does
is the Golden Ratio, about 1.618033988, so this algorithm does
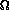 (
( n) additions. This exponential behavior is very
inefficient.
n) additions. This exponential behavior is very
inefficient.
We can do much better with dynamic programming.
Our problem satisfies the optimal substructure property: each
solution is the sum of two other solutions.
It also satisfies the overlapping subproblems property: each
solution includes many sums of previous solutions.
Thus we can use the 3rd and 4th steps to design an algorithm that
uses the precomputed information.
Using a dynamic programming technique called memoization,
we can make the recursive algorithm much faster. We assume there
is an array A of integers whose first and second elements
have been initialized to 1, and there is an integer called unknown,
initially two, that keeps track of the index of the least Fibonacci
number whose value is not known:
F (n)
if n < unknown then return A[n]
A[n] = F(n-2) + F(n-1)
return A[n]
This algorithm is very similar to the previous one, but it uses
the array A as a sort of "scratch" area to record previous
results, rather than recompute compute them.
What is the running time of this recursive algorithm?
If Fi is computed, it is stored in the array
and never recomputed, so the algorithm basically traces a path from
root to rightmost leaf of the tree, adding up all the results at each level
in one addition. Thus the algorithm runs in time
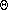 (n). This is much better
than the exponential-time algorithm.
(n). This is much better
than the exponential-time algorithm.
What about the storage required? The first algorithm seems to have an
advantage, since the second requires an array of size at least n
to work. But even the first algorithm uses O(n)
storage, since a stack frame is consumed for each of the n levels
of recursion.
This memoization technique can be applied to many recursive algorithms,
and can really speed up your programs. Once you have computed
em>Fn, finding the value of em>Fi
where i < n takes
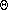 (1) time, since it is just an
array access! This technique can speed up programs even when the recursive
algorithm to compute a function is no slower than the memoized algorithm;
the first computation from both algorithms may take, say,
(1) time, since it is just an
array access! This technique can speed up programs even when the recursive
algorithm to compute a function is no slower than the memoized algorithm;
the first computation from both algorithms may take, say,
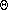 (n),
but each subsequent memoized lookup is just
(n),
but each subsequent memoized lookup is just 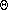 (1).
(1).
(It turns out when analyzing numerical algorithms like this, we need to
be a little more careful and look at the asymptotic cost of multiplying
and storing large numbers. In C, we quickly exhaust the 32 or 64 bits
modern compilers give us for integers and must move to a large integer
representation. Then the time needed to multiply m-bit numbers
becomes important.)
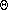 (2n) nodes. While this tree is not quite that big, it is
very close. There are Fn 1's as leaves of the
tree, so at least that many additions. From equation 2.15 in the book,
we can tell that Fn =
(2n) nodes. While this tree is not quite that big, it is
very close. There are Fn 1's as leaves of the
tree, so at least that many additions. From equation 2.15 in the book,
we can tell that Fn =
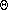 (
( n), where
n), where  is the Golden Ratio, about 1.618033988, so this algorithm does
is the Golden Ratio, about 1.618033988, so this algorithm does
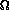 (
( n) additions. This exponential behavior is very
inefficient.
n) additions. This exponential behavior is very
inefficient.