But sometimes asymptotic analysis fails us. For instance:
#include <stdio.h>
#include <time.h>
#define MEMSIZE (1<<24) /* 2 to the 24 power, about 16 million */
int main () {
register int i, count, n;
register char *p;
int c1, c2;
double t;
/* allocate a bunch of bytes */
p = (char *) malloc (MEMSIZE);
/* how many memory accesses to do */
n = MEMSIZE * 10;
/* count the number of memory accesses done */
count = 0;
/* start indexing the array at element 0 */
i = 0;
/* read number of clock ticks so far */
c1 = clock ();
/* do n memory accesses */
while (count < n) {
/* write 0 to memory; this is the memory access we're timing */
p[i] = 0;
/* go to next index in array of bytes */
i++;
/* loop around if we go out of bounds */
if (i >= MEMSIZE) i = 0;
/* one more memory access */
count++;
}
/* what time is it now? */
c2 = clock ();
/* how many clock ticks have passed? */
t = c2 - c1;
/* how many seconds is that? */
t /= CLOCKS_PER_SEC;
printf ("%f seconds\n", t);
/* how many seconds to access one byte? */
t /= n;
/* multiply by a billion to get nanoseconds */
printf ("%f nanoseconds per access\n", t * 10e9);
exit (0);
}
We can (somewhat) safely ignore the counting code as not contributing a significant amount of time to the time measured; those variables are usually stored in CPU registers, which have a much faster access time than RAM.
I ran this program on a Pentium 200MHz computer with 64MB RAM. It reported memory access (write) time as 350 nanoseconds. That's not too bad. I tried it on an old SPARCstation 10 and got 913 nanoseconds. I tried it on a very old 486DLC/33 and got about 4600 nanoseconds, yikes. I used the highest possible level of optimizations for gcc on each platform.
Is this a reliable way of measuring memory speed? No; almost all of the memory accesses are consecutive. In practive, memory accesses don't come this way. Let's look at a more robust program that measures access for different strides or distances between accesses:
#include <stdio.h>
#include <time.h>
#define MEMSIZE (1<<24)
int main () {
register int i, count, n;
register char *p;
int c1, c2, k;
double t;
p = (char *) malloc (MEMSIZE);
n = MEMSIZE * 10;
for (k=1; k<100; k++) {
count = 0;
i = 0;
c1 = clock ();
while (count < n) {
p[i] = 0;
i+=k;
if (i >= MEMSIZE) i = 0;
count++;
}
c2 = clock ();
t = c2 - c1;
t /= CLOCKS_PER_SEC;
printf ("k = %d\n", k);
printf ("%f seconds\n", t);
t /= n;
printf ("%f nanoseconds per access\n", t * 10e9);
fflush (stdout);
fflush (stderr);
}
exit (0);
}
This time, instead of timing for just one stride, i.e., 1, I timed it
for memory accesses where the distance between each varied from 1 to 100.
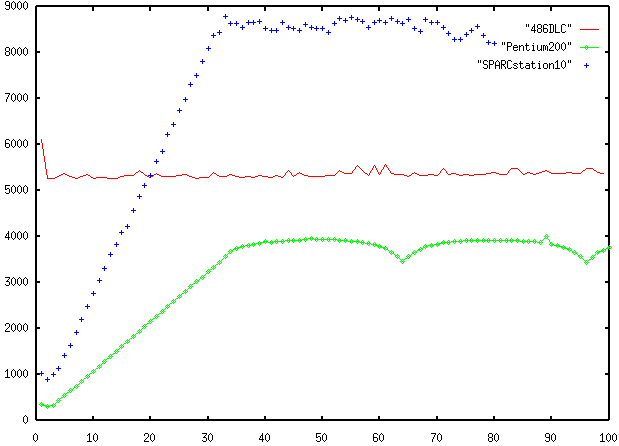
Here are the results for all three computers. The x-axis
is the stride, and the y-axis is the average time for
a memory access in nanoseconds:

The Pentium gets as bad as 4000 nanoseconds. The 486, with its tiny 1K cache, does about the same for every stride. The SPARCstation starts off pretty good but reaches a plateau at almost 10,000 nanoseconds, being beat by the little 486!
The Principal of LocalityThis is how computer architects build computers, with this idea in mind. If your programs follow this principle, they will run fast. If they don't, they will run slowly. The principal of locality is also often stated as the 90/10 rule: 90% of a programs execution will concern 10% of the programs code.
(From Hennessy and Patterson, Computer Architecture: A Quantitative Approach
- Temporal Locality (locality in time): If an item is referenced, it will tend to be referenced again soon.
- Spatial Locality (locality in space): If an item is referenced, nearby items will tend to be referenced soon.
Here is an example. This C function adds two N by N matrices, placing the result in a third:
void add (int A[N][N], int B[N][N], int C[N][N]) {
int i, j, k, sum;
for (i=0; i<N; i++)
for (j=0; j<N; j++)
C[i][j] = A[i][j] + B[i][j];
}
Note that the loop takes
 (N2) time
asymptotically.
I ran a program using this C function to add two 256 by 256 matrices
together, computing the array access time for the two reads and one write.
I got an average 367 nanoseconds for access to a single integer array
element, which is pretty good considering an integer is four bytes.
The program ran the loop 500 times, taking 3.61 seconds to complete.
Then I switched the two loops:
(N2) time
asymptotically.
I ran a program using this C function to add two 256 by 256 matrices
together, computing the array access time for the two reads and one write.
I got an average 367 nanoseconds for access to a single integer array
element, which is pretty good considering an integer is four bytes.
The program ran the loop 500 times, taking 3.61 seconds to complete.
Then I switched the two loops:
void add (int A[N][N], int B[N][N], int C[N][N]) {
int i, j, k, sum;
for (j=0; j<N; j++)
for (i=0; i<N; i++)
C[i][j] = A[i][j] + B[i][j];
}
and ran the program again. I got 2774 nanosecond access time and the whole
thing took 27.27 seconds. The algorithm was now 755% slower! Why?
In C, two-dimensional arrays are laid out in row-major format. That is, 2D arrays are basically 1D arrays of rows, so that A[i][j] is right next to A[i][j+1] and A[i][j-1] in memory.
When I let the inner loop take j from 0 to N-1, all of those memory accesses were consecutive, following the principle of locality. The first memory access brought most of the rest of the data into the L1 cache, so the rest of the memory accesses were very fast.
When I switched the two loops, memory accesses that occurred one after another accesses different rows, whose elements were far apart in memory. Each access had to go to slower RAM to find the memory, and didn't use the caches at all.
This illustrates an important point: when you are writing an algorithm, try as much as you can to stay "in cache," i.e., if you have a choice, keep memory accesses done one after another near each other in memory.
There is a lot more to the memory hierarchy than we have seen here, that you will see in a computer architecture class. Different computers have different policies about what goes in the cache, how big the cache is, etc. However, if you stick to the principal of locality, your programs should run faster no matter what the architecture is.
OF COURSE, this doesn't mean we can now ignore asymptotic notation. Quicksort still beats bubble sort even though bubble sort obeys the principle of locality much more than Quicksort.